和是偶数的可能性小——不对吗？

湖北省荆门市钟祥市郢中街办莫愁小学  周俊玲

评析 湖北省荆门市小学数学名师工作室主持人  周齐才

【案例】  

片段一： 

     “有分别写着1～20的20张卡片，任意抽两张，将卡片上的数相加，和是双数的可能性小。（   ）”这是人教版小学数学五年级上册《长江作业本》同步练习册第38页第四单元《可能性》第1课时中的一道判断题。

       前段时间，我在教学《可能性》这个知识时，遇到了这道题。起初，很多学生和同事都一致认为和是偶数的可能性大，这个题判“×”。理由是：奇数+奇数=偶数，偶数+偶数=偶数，奇数+偶数=奇数。两数相加的和有3种情况，而偶数占2种，故判这道题为×。乍一听好像有道理，但仔细一推敲却不认同，我觉得此题并不是他们说的这样简单，应该先根据“组合”，看有多少个和，再看这些和中奇数和偶数分别有多少个。顺着这个思路，我一一列举后发现：两数相加的和有190个，偶数占90个，奇数占100个。和是偶数的可能性小，所以应判“P”。

       当我和身边的同事交流自己的观点时，有的老师说：这个题哪有这么复杂，这么多数字，举例太麻烦了，你想多了。有的老师说：这是《长江作业本》中的题，扫码得知答案是×，搜题软件也说是×，我们应该相信答案；还有的老师说：一个判断题而已，你也太较真了。

面对同事的反驳和不屑，我再次陷入沉思：“如果真那样分析的话，岂不是所有这类题的结论都是和为偶数的可能性大？” 

       如果觉得这个题数字多，太复杂，那我们就先从简单的入手：：从写有1、2、3、4的四张卡片中，任意抽两张，将卡片上的数字相加，和是偶数的可能性（   ）。运用组合的知识，两数相加，可以得到：1+2=3、1+3=4、1+4=5、2+3=5、2+4=6、、3+4=7，和是偶数的有2个，和是奇数的有4个，和是偶数的可能性小。其实仔细研究，我们会发现：2+4=6运用的是“偶数+偶数=偶数”，1+3=4运用的是“奇数+奇数=偶数”，剩余4个奇数的和是运用“奇数+偶数=奇数”得到的。会不会是凑巧？我又试了几组：1、2、3、4、5、6和2、3、7、10、13、14。无论是运用组合知识，通过一一列举，还是根据奇偶相加比较，最终都是和为偶数的可能性小。

       再回到作业中的那道题，这道题应该与教材第50页“综合与实践”课“掷一掷”中的掷骰子的教学思路如出一辙。虽然从理论上分析两数相加的和可以通过“奇数+奇数、偶数+偶数、奇数+偶数”这3种途径得到，但最终和只有奇数、偶数2种情况。其中：奇数+奇数时，可以得到45个偶数的和；偶数+偶数时，也可以得到45个偶数的和；奇数+偶数时，能得到100个奇数的和。当然我们也可以用列表的方法把这些和一一排列出来（具体过程附后）。这样一来，两数相加的和就有190个，偶数占90个，奇数占100个。确实和是偶数的可能性小。 

      反复验证后，最终，我得出一个结论：无论是数字少，还是数字多，其实和都只有奇数、偶数2种，都可以通过奇数+偶数、偶数+偶数、奇数+奇数这3种途径得到，但是要比较和的奇偶性，必须看所有和中奇数与偶数分别有多少个。当我再次和同事探讨时，我详细地讲解了自己的思路，他们又感觉是这个理，不再反驳。

      一一列举，分析：

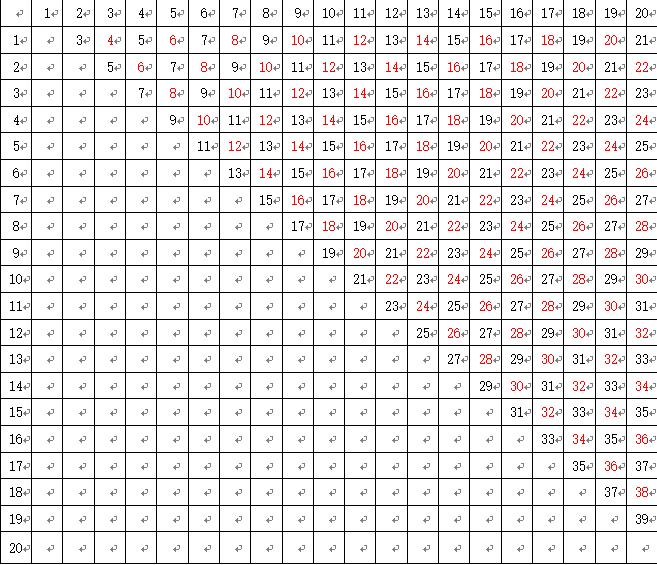
       和是奇数：100个                     和是偶数：90个（可能性小）

        分类列举，分析：

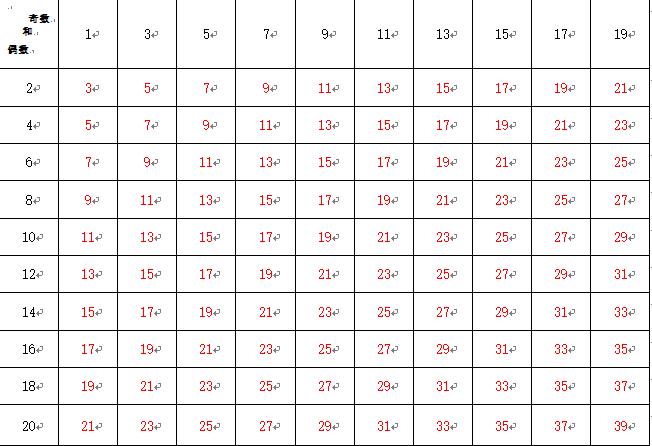
分析：

     1.   表中把1-20这20个自然数分成10个奇数，10个偶数。根据“奇数+偶数=奇数”可知：有10×10=100个奇数的和。

     2.   从2、4、6、8、10、12、14、16、18、20这10个偶数中任意取两个数相加，根据“偶数+偶数=偶数”可知：共有9+8+7+6+5+4+3+2+1=45个偶数的和。

    3.   从1、3、5、7、9、11、13、15、17、19这10个奇数中任意取两个数相加，根据“奇数+奇数=偶数”可知：也有9+8+7+6+5+4+3+2+1=45个偶数的和。

这样，一共有45×2=90个偶数的和。

故：和是偶数的可能性小。

片段二：

      有了清晰的思路，接下来在给学生讲解这道题时，一开始我没有急着否定他们的观点，而是先给了另一组数据“1、2、3、4”，引导他们讨论交流，思维活跃的同学迅速有了想法：1+2=3、1+3=4、1+4=5、2+3=5、2+4=6、3+4=7，和是偶数的有2个，和是奇数的有4个，和是偶数的可能性小。思路打开了，“同学们能不能自己试着写一组数字，小组内交流一下？”顺势利导，我让学生自己尝试研究。

   很快，大多数同学从原来的思维胡同跳出来了，“这不就是利用组合的知识，先把两数相加的和有序地列举出来吗？”有几个同学兴奋地说到。“说得很好！如果把这4张卡片改为1～20张卡片呢？”我看到有的同学立马按照“组合”的方法，耐心细致地在写着两数相加的算式，几分钟后，“周老师，这也太多了，我都写了好多了还没写完。”“是的，太多了。”有些不耐烦的同学叫嚷着。“如果把每一个算式都完整地写出来，确实很麻烦，借助表格可以大大提高效率，大家再想想。”“哦，我们可以像掷骰子那样用表格来一一列举。”“学以致用，老师给你们点赞！”接下来，我给每一个小组发了一张事先准备好的表格，让他们小组讨论，共同完成表格……

  “利用表格虽然稍微快一点，但同学们不觉得这样也有些麻烦吗？这可是只有20张卡片？如果再多些卡片呢？除了一一列举，到底还有没有藏着什么规律呢？大家想不想继续探究一下？”“想！”“那咱们还是先回到简单的1-4张卡片上来。”接下来，我引导学生把4张卡片分成1和3两个奇数、2和4两个偶数，再根据“奇数+偶数=奇数”得到奇数的和有2×2=4个，再根据“偶数+偶数=偶数”、“奇数+奇数=偶数”得到偶数的和共有2个，得出和是偶数的可能性小。“1-6张卡片呢？”同学们迅速自己试着分类进行分析。“周老师，我发现把这6个数字分成3个奇数，3个偶数后，直接用3×3就可以知道有9个奇数的和；而从1、3、5这3个奇数中任选两个数字相加时，可以得到2+1=3个偶数的和；从2、4、6这3个偶数中任选两个数字相加时，也可以得到2+1=3个偶数的和。一共有6个偶数的和，和是偶数的可能性小。”“我也是这样想的，我觉得这样分类来计算很简单。”“同学们的发现非常有价值！当我们遇到数字比较繁多的数学问题时，可以从简单的数字入手分析，找寻其中的规律，总结解题的方法，再利用规律举一反三。下面我们就利用这个规律一起来分析一下1~20张卡片中的奥秘。”……

  “如果是1~100张卡片、1~n张卡片呢？同学们想不想一探究竟？”课后，有兴趣的同学快速围到我身边，和我交流自己的想法。“看来你们这节课的收获不小啊，老师十分期待你们的探究结果哟！”看到孩子们兴趣盎然的样子，一丝欣慰之情在我的心底油然而生，我很高兴：有一颗“兴趣”的种子在孩子们的头脑中萌芽了！

片段三：

     2021年11月4日，我参加了湖北省“校对县”精准帮扶培训活动，有幸和专家团队的老师零距离交流。交流会上，我大胆地向周齐才校长请教了这个问题，“看来你是一个功底很深的数学教师，坚持自己的观点，‘不唯书、不唯上、只唯实’，我同意你的观点，这个题的确和掷骰子的算理类似。这是一个非常好的教学案例，我建议你把这个案例写出来。”还没等我问完，周校长已迫不及待地答道。在场参训的其他老师也提出了和同事开始一样的质疑，他认为：运用高中数学里的组合知识，和是偶数的可能性小，而小学阶段应该按照奇偶相加来理解，和是偶数的可能性大。“同一道判断题，怎么会有两种相反的答案呢？”周校长反问道。

      第一次这样面对面向专家请教，能得到周校长的鼓励和肯定，内心一丝小窃喜，好似得到了权威机构认证一样，埋在我心中的疑云彻底消散了，也让我更加坚定了自己最初的想法。

【反思】

     1、教师要勇于提出质疑。

     数学是一门严谨的学科，容不得半点含糊。

     在教学中，如果遇到这种有争议的数学问题时，一定要大胆质疑，不要一味相信作业中的答案，也不要被他人左右自己的思路。还要认真思考，反复研究，通过举例或推理验证等方法得出正确结论。

      正如周校长所说：大多数老师遇到这样的问题，也许就简单略过了，能够执着钻研的最后可能就成了数学家。作为一名普通的数学教师，即便不能成为数学家，我们也要有自己的思想，努力用自己的思想去引领学生“思”、“辨”、“理”，和学生一起探讨数学的奥秘。。

    2、教师要灵活运用数学方法。

    猜想、转化、推理、枚举、化繁为简等都是学习数学的好方法。当我们遇到数据较大或较多的数学问题时，不妨先从小数据入手分析。这次培训学习，袁志刚老师和周金凤老师执教的《植树问题》一课，都把例题中的数字由大变小，效果甚好！     

    教师不仅要灵活运用数学方法，还要善于运用数学思想教学生学习数学。当一个问题比较复杂时，“回到最简单的情形”，这是华罗庚教授所倡导的！这样更能看清问题的本质。正是基于这种数学思想，上面片段二中，我也是先引导学生从小数据着手分析，待学生有了初步感知后，我又大胆放手让他们自己试着写一组数字研究，再引导学生由简到繁找寻这类问题蕴含的规律，最后拓展提升：“1~100张卡片、1~n张卡片呢？”由始至终，充分激发学生的学习兴趣和探究欲望，留给学生充足的探究空间和时间，让他们亲历知识的形成过程，更好地掌握数学技能，学习数学，体验成功的乐趣。又何乐而不为呢！

    3、教师要成为终身学习者。              

习近平总书记在庆祝第30个教师节到来时，勉励全国广大教师“做好老师，要有扎实学识”。扎实的知识功底、过硬的教学能力、勤勉的教学态度、科学的教学方法是老师的基本素质，其中知识是根本基础。

教师作为传道、授业、解惑者，要想给学生一碗水，自己就要有一桶水；要做一名新时代的好老师，更要有一潭活水，要为学生“引来水源”，教会孩子们学习的方法和思想。陶行知先生说：“出世便是破蒙，进棺材才算毕业。”这就要求老师始终处于学习状态，站在知识发展的前沿，刻苦钻研、严谨笃学，不断充实、拓展、提高自己。   

     【评析】这是一个很好的教学案例，主要体现在：

      1.选题具有挑战性。在作业中善于发现问题，从争议入手，用科学方法澄清疑惑，研究的过程也具有趣味性、探究性。

      2.方法具有科学性。解决问题的方法、所涉及的知识都在学生能力所及范围内，即学生最近发展区内，通过问题的探究，让学生经历一个知识发生、发展全过程，积累数学活动经验；当一个问题比较复杂时，“回到最简单的情形” 这是华罗庚教授所倡导的！这样更能看清问题的本质；通过列表、分类讨论等多种方法，得出结论，层层递进，有理有据，让学生在获得知识的同时，也学到探究问题的方法。

     3.教师具有示范性。教师引领学生“不唯书、不唯上、只唯实”，是一个优秀教师的科学精神。引导学生敢于质疑，不迷信权威，就是创新意识的萌芽。

                                                 2021.11.10

周齐才：湖北省骨干教师，湖北省教学数学专业委员会理事，荆门市名师，荆门市小学数学名师工作室主持人。现任荆门市石化第一小学副校长。

QQ：439622368    电话：13986976676