随着新课程改革在全国各地的不断深入,近年来在全国各省市的中考试题出现了许多新题型,这些设计独特的新题型恰好体现新课程改革的最终目的——激发学生的创新思维,培养学生创新意识,提高学生的数学应用能力.本文以2006年全国各省市课改实验区的中考试题为例,探析新题型的特点及其解法,供同学们参考.
一、自编自解的开放型
例1(宁夏回族自治区课改实验区)如图1,点A、B、D、E在圆上,弦AE的延长线与弦BD的延长线相交于点C,给出下列三个条件:
①AB是圆的直径;②D是BC的中点;③AB=AC.
请在上述条件中选取两个作为已知条件,第三个作为结论,写出一个你认为正确的命题,并加以证明.
解:命题一:条件:AB是圆的直径,D是BC的中点.结论:AB=AC. 证明:连结AD ∵AB是圆的直径 ∴∠ADB=90°,即AD⊥BC, 又∵D是BC的中点,∴BD=DC,∴AB=AC. 命题二:条件:AB是圆的直径,AB=AC.结论:D是BC的中点. 命题三:条件:D是BC的中点,AB=AC.结论:AB是圆的直径. | 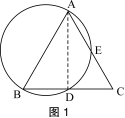 |
评析:此题一改过去统一模式的定向思维为灵活多变的开放思维,这些自编自解的开放型试题,是实施数学创新教育的一个切入点,是新课程改革的一个新亮点.解决这类试题,必须要有扎实全面的基础知识,并熟悉每个知识点的横向与纵向的联系,才能自编自解.
对应训练(昆明市课改实验区)已知:如图2,AB//DE,且AB=DE. <1>请你只添加一个条件,使△ABC≌△DEF,你添加的条件是_____. <2>添加条件后,证明△ABC≌△DEF. | 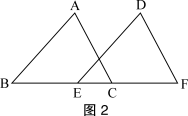 |
二、实际应用型
例2(贵阳市课改实验区)如图3,这是一个供滑板爱好者使用的U型池,该U型池可以看成是一个长方体去掉一个“半圆柱”而成,中间可供测行部分的载面是半径为4m的半圆,其边缘AB=CD=20m,点E在CD上,CE=2m,一滑板爱好者从A点滑到E点,则他滑行的最短距离为______m(边缘部分的厚度忽略不计,结果保留整数).
解:将图3“展开”成平面图,如图4 连结AE,则AE的长为所求的最短距离,在Rt△AED中,DE=20-2=18m,AD=1/2·2π·4=4πm,由勾股定理得: 评析:本题设计独特,来源于学生生活中的事例,体现“让数学走进生活”的新理念,让学生体验数学来源于生活,服务于生活的辩证思想,它的解题关键是把生活问题巧妙转化为数学问题,本题通过构建Rt△,问题就迎韧而解. |
|
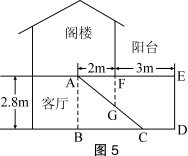
对应训练(安徽省课改实验区)汪老师要装修自己带阁楼的新居(如图5为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m,他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m,请你帮助汪老师解决下列问题:
<1>要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是多少米? <2>在<1>的条件下,为保证上楼时的舒适感,楼梯的每个台阶高要小于20cm,每个台阶宽要大于20cm,问汪老师应该将楼梯建几个台阶?为什么? |
|
三、猜想、探究型
例3(贵阳市课改实验区)两条平行直线上各有n个点,用这n对点按如下规则连接线段.
① 平行线之间的点在连线段时,可以有共同的端点,但不能有其他交点;
② 符合①要求的线段必须全部画出.

图6展示了当n=1时的情况,此时图中三角形的个数为0;
图7展示了当n=2时的情况,此时图中三角形的个数为2;
<1>当n=3时,请在图8中画出使三角形个数最少的图形,此时图中三角形的个数为___;
<2>试猜想当有n对点时,按上述规则画出的图形中,最少有多少个三角形?
<3>当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
解:<1>当n=3时,图8中三角形的个数为4个;
<2>当有n对点时,最少有2(n-1)个三角形;
<3>当n=2006时,2×(2006-1) =4010个,即最少可以画出4010个三角形.
评析:猜想与探究是数学发现过程中的一种创造性思维,关于猜想、探究的试题已成为近年来中考命题的热点.解决此类试题一般要进行观察、实验、分析、比较、联想、类比,再进行综合与归纳,从特殊到一般再到特殊进行思考分析.
对应训练(安徽省课改实验区)老师在黑板上写出三个算式:52-32=8×2,92-72=8×4,152-32=8×27,
王华接着又写了两个具有同样规律的算式:112-52=8×12,152-72=8×22,……
<1>请你再写出两个(不同于上面算式)具有上述规律的算式;
<2>用文字写出反映上述算式的规律;
<3>证明这个规律的正确性.
四、图形运动型
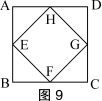
例4(宁夏回族自治区课改实验区)在边长为6cm的正方形ABCD中,点E、F、G、H分别按A→B、B→C、C→D、D→A的方向同时出发,以1cm/s的速度匀速运动,如图9.
<1>在运动中,点E、F、G、H所形成的四边形EFGH为( ). A、平行四边形 B、矩形 C、菱形 D、正方形 |
|
<2>四边形EFGH的面积S(cm2)随运动时间t(s),变化的图象大致是( ).

< 3>写出四边形EFGH的面积S(cm2)关于运动时间t(s)变化的函数关系式,并求运动几秒钟时,面积最小?最小值是多少?
解:<1>D,<2>B,<3>AE=1×t=t,AH=6-t,S=EH2=AE2+AH2=t2+(6-t) 2=2t2-12t+36 ∴S=2(t-3) 2+18 ∴当运动3秒钟时,S有最小值为18 cm2.
评析:运动观点的思想渗透到数学之中,给数学中考命题带来许多新的创意. “动态型”试题往往“动”中有“静”,是近年来中考的“必考”题型.解决此类试题突破口是“静”,即构建“恒等”关系,从而解题.
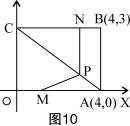
对应训练(黄冈市课改实验区)如图10,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(4,0)、(4,3),动点M、N分别从点O、B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连结MP,当两动点运动了t秒时,
<1>P点的坐标为(____,____)(用含t的代数式表示); <2>记△MPA的面积为S,求S与t的函数关系式(O<t<4); <3>当t=_____秒时,S有最大值,最大值是______; <4>若点Q在y轴上,当S有最大值且△QAN为等腰三角形时,求直线AQ的解析式. |
|
五、判断说理型
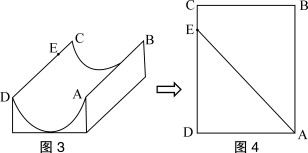
例5(乌鲁木齐市课改实验区)如图11,萌萌将菱形ABCD绕点A按逆时针方向旋转180°得到了菱形AB1C1D1,连结BD1、D1B1、D1B、DB,她通过观察发现四边形BDB1D1是矩形,请你判断她的推测是否正确,若正确请给予证明;若不正确,请说明理由.
解:萌萌的推测是正确的.证明:菱形AB1C1D1与菱形ABCDD关于菱形ABCD关于点A成中心对称,∴AB=AB1, AD=AD1,∴四边形BDB1D1是平行四边形.又∵AB=AD,∴DD1 =BB1,∴平行四边形BDB1D1是矩形. | 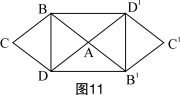 |
评析:判断说理题是近年新兴的中考试题,它要求学生先进行分析与判断,一般对“正确与否”或“存在与否”进行定论后,再加以证明,它的特点是设下情境,让学生“参与”其中,它能很好考查学生的分析能力、判断能力、表达能力.其解题关键是判断必须准确,否则全功尽费.
对应训练(沈阳市课改实验区)如图12,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE;②AF⊥DE(不需要证明).

<1>如图13,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”);
<2>如图14,若点E、F分别在正方形ABCD的边CB、DC的延长线上,且CE=DF,此时的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
<3>如图15,在<2>的基础上,连结AE和EF,若点M、N、P、Q分别AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
六、观察、归纳型
例6(沈阳市课改实验区)观察下列等式:21=2;22=4;23=8;24=16;25=32;26=64;27=128,……通过观察,用你所发现的规律确定22006的个位数字是____.
解:依题意可得2n(n≥1)的个位数字是周期性循环出现的。
∵ 22006=24×501+2,∴ 22006的个位数字是4,故填4.
评析:通过观察,发现数量或图形的规律,从感性认识向理性认识飞跃,这是发现过程中的重要思想方法,这既是考查学生能力水平的试题,又是通过知识的迁移、类比、转化、激发学生探索新知识的积极性和主动性.解决此类试题关键是根据已知题目的具体情况,细心观察、认真分析、大胆推测、把握规律.
对应训练(昆明市课改实验区)观察图16至图19中小圆圈的摆放规律,并按这样的规律继续摆放,记n个正方形中小圆圈的个数为m,则m=______(用含n的代数式表示).

七、方案最优型
例7(贵阳市课改实验区)某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
<1>符合公司要求的购买方案,有哪几种?请说明理由;
<2>如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1500元,那么应选择以上哪种购买方案?
解:<1>设轿车要购买X辆,那么面包车要购买(10-X)辆,由题意得:7X+4(10-X)≤55,解得:X≤5,又X≥3,则X=3,4,5,即采购方案有三种:方案一:轿车购买3辆,面包车购买7辆;方案二:轿车购买4辆,面包车购买6辆;方案三:轿车购买5辆,面包车购买5辆.
<2>方案一的日租金为:3×200+7×110=1370;方案二的日租金为:4×200+6×110=1460;方案三的日租金为:5×200+5×110=1550,为保证日租金不低于1500元,应选择方案三.
评析:这类试题正好体现“人人学有价值的数学”的课改新理念,反映数学是与学生的现实生活及已有的知识体验密切相关,让学生感受数学“学有所用”.解决这类题的关键是在理解题目背景的基础上,寻找已知量与未知量之间的内在联系,建立恰当的数学模型,如方程(组)模型、函数模型、不等式(组)模型等等.
对应训练(昆明市课改实验区)云南省公路建设发展速度越来越快,通车总里程已位居全国第一,公路的建设促进了广大城乡客运的发展,某市扩建了市县级公路,运输公司根据实际需要计划购买大、中两型客车共10辆,大型客车每辆价格为25万元,中型客车每辆价格为15万元.
<1>设购买大型客车x(辆),购车总费用为y(万元),求y与x之间的函数表达式;
<2>若购车资金为180万元至200万元(含180万元和200万元),那么有几种购车方案?在确保交通安全的前提下,根据客流量调查,大型客车不能少于4辆,此时如何确定购车方案可使该运输公司购车费用最少?
由上述可见,呈现在近年来的中考新题型设计独特,构思新颖,贴近生活,确实令我们耳目一新。当然新题型远不止上述几例,以上的例子和训练,只是抛砖引玉之意,希望它能给同学们在中考复习中有所帮助.





6